Mean-Field Dynamics
In this tutorial we discuss to use TEMPO and the process tensor approach to compute the dynamics of a many-body system of the type introduced in [FowlerWright2021] (arXiv:2112.09003).
launch binder (runs in browser),
read through the text below and code along.
Contents:
Background and introduction
many-body system and environment Hamiltonians
system Hamiltonian and field equation of motion after the mean-field reduction
Creating time-dependent system with field and bath objects
TEMPO computation for single dynamics
PT-TEMPO computation for multiple sets of dynamics
We firstly import OQuPy and other useful packages:
import sys
sys.path.insert(0,'..')
import oqupy
import numpy as np
import matplotlib.pyplot as plt
Check the current OQuPy version; mean-field functionality was introduced in version 0.3.0.
oqupy.__version__
'0.3.0'
The following matrices will be useful below:
sigma_z = oqupy.operators.sigma("z")
sigma_plus = oqupy.operators.sigma("+")
sigma_minus = oqupy.operators.sigma("-")
1. Background and introduction
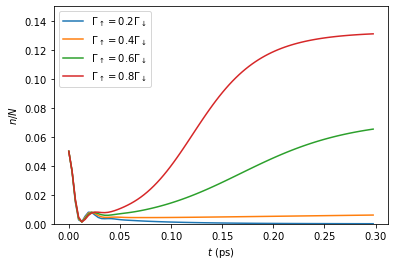
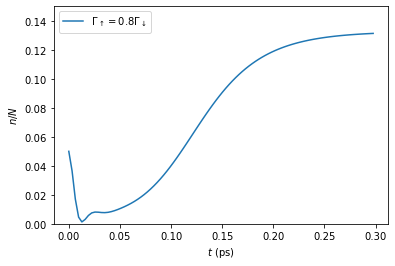
Our goal will be to reproduce a line from Fig. 2a. of [FowlerWright2021] (arXiv:2112.09003) which shows the photon number dynamics for the driven-dissipative system of molecules in a single-mode cavity.
Many-body system and environment Hamiltonian
The Hamiltonian describing the many-body system with one-to-all light-matter coupling is
Together with the vibrational environment of each molecule,
This is taken to be a continuum of low frequency modes with coupling characterized by a spectral density with a ‘Gaussian’ cut-off
where \(\alpha=0.25\) is the unit-less coupling strenght and \(\hbar \nu_c = 0.15\) eV is a cutoff frequency for the environment of the BODIPY-Br molecule considered in the Letter. For the numericla simulation we here choose to express all frequencies as angular frequencies in the units of \(\frac{1}{\text{ps}}\) (setting \(\hbar = k_B = 1\)) and all times in units of ps. The parameters relevant to Fig. 2a. given in those units are:
\(\nu_c = 0.15 \text{eV} = 227.9 \frac{1}{\text{ps}}\) … environment cutoff frequency
\(T = 300 \text{K} = 39.3 \frac{1}{\text{ps}}\) … environment temperature
\(\omega_0 = 0.0 \frac{1}{\text{ps}}\) … two-level system frequency *
\(\omega_c = -0.02 \text{eV} = -30.4 \frac{1}{\text{ps}}\) … bare cavity frequency
\(\Omega = 0.2 \text{eV} = 303.9 \frac{1}{\text{ps}}\) … collective light-matter coupling
together with the rates
\(\kappa = 15.2 \frac{1}{\text{ps}}\) … field decay
\(\Gamma_\downarrow = 30.4 \frac{1}{\text{ps}}\) … electronic dissipation
\(\Gamma_\uparrow \in (0.2\Gamma_\downarrow, 0.8\Gamma_\downarrow)\) … electronic pumping
The latter appear as prefactors for Markovian terms in the quantum master equation for the total density operator
As indicated, it is the pump strength \(\Gamma_\uparrow\) that is varied to generate the different lines of Fig. 2a. In this tutorial we generate the \(\Gamma_\uparrow=0.8\,\Gamma_\downarrow\) line using the TEMPO method, and then the Process Tensor approach to calculate all of the lines efficiently.
The following code box defines each of the above parameters.
* N.B. for calculating the dynamics only the detuning \(\omega_c-\omega_0\) is relevant, so we set \(\omega_0=0\) for convenience.
alpha = 0.25
nu_c = 227.9
T = 39.3
omega_0 = 0.0
omega_c = -30.4
Omega = 303.9
kappa = 15.2
Gamma_down = 30.4
Gamma_up = 0.8 * Gamma_down
System Hamiltonian and field equation of motion after the mean-field reduction
The mean-field approach is based on a product-state ansatz for the total density operator \(\rho\),
where \(\text{Tr}_{\otimes{i}}\) denotes a partial trace taken over the Hilbert space of all two-level systems and \(\text{Tr}_{a, \otimes{j\neq i}}\) the trace over the photonic degree of freedom and all but the \(i^{\text{th}}\) two-level system. As detailed in the Supplement of the Letter, after rescaling the field \(\langle a \rangle \to \langle a \rangle/\sqrt{N}\) (\(\langle a \rangle\) scales with \(\sqrt{N}\) in the lasing phase), the dynamics are controlled by the mean-field Hamiltonian \(H_{\text{MF}}\) for a single molecule,
together with the equation of motion for the field \(\langle a \rangle\),
Therefore in order to calculate the dynamics we need to encode the field’s equation of motion in addition to the Hamiltonian for a single two level-system \(\rho_i\) (which we identify as the ‘system’ in our TEMPO computation).
In OQuPy, the relevant classes and methods hence all have the
WithField suffix: TimeDependentSystemWithField,
DynamicsWithField, TempoWithField (TEMPO) and
compute_dynamics_with_field() (PT-TEMPO).
2. Creating time-dependent system with field and bath objects
A TimedependentSystemWithField object requires two physical inputs:
a Hamiltonian, which is a function of time \(t\) and field
\(\langle a \rangle\) (in that order), and a equation of motion for
the field, which is a function of time \(t\), system state
\(\rho_i\) and field \(\langle a \rangle\). Positional arguments
are used for these functions, so the order of arguments matters whilst
their name does not:*
def H_MF(t, a):
return 0.5 * omega_0 * sigma_z +\
0.5 * Omega * (a * sigma_plus + np.conj(a) * sigma_minus)
def field_eom(t, state, a):
expect_val = np.matmul(sigma_minus, state).trace()
return -(1j * omega_c + kappa) * a - 0.5j * Omega * expect_val
Note \(\rho_i\) is provided as a \(2\times2\) matrix, hence to compute the expectation \(\langle \sigma^- \rangle\) we used matrix multiplication with \(\sigma^-\) and took the trace. It’s a good idea to test these functions:
test_field = 1.0+1.0j
test_time = 0.01
test_state = np.array([[0.0,2j],[-2j,1.0]])
print('H_eval =', H_MF(test_time, test_field))
print('EOM_eval =', field_eom(test_time, test_state, test_field))
H_eval = [[ 0. +0.j 151.95+151.95j]
[151.95-151.95j 0. +0.j ]]
EOM_eval = (258.29999999999995+15.2j)
Secondly, we need to specify Lindblad operators for the pumping and dissipation processes:
gammas = [ lambda t: Gamma_down, lambda t: Gamma_up]
lindblad_operators = [ lambda t: sigma_minus, lambda t: sigma_plus]
Here the rates and Lindblad operators must be callables taking a single argument - time - even though in our example there is no time-dependence (see * below). The system-field object is then constructed with
system = oqupy.TimeDependentSystemWithField(
H_MF,
field_eom,
gammas=gammas,
lindblad_operators=lindblad_operators)
Correlations and a Bath object are created in the same way as in any other TEMPO computation (refer to preceding tutorials):
correlations = oqupy.PowerLawSD(alpha=alpha,
zeta=1,
cutoff=nu_c,
cutoff_type='gaussian',
temperature=T)
bath = oqupy.Bath(0.5 * sigma_z, correlations)
* In particular both functions must have a first argument
representing time, even if the problem - as here - has no explicit
time-dependence (for codebase simplicity there is no SystemWithField
class).
3. TEMPO computation for single dynamics
For our simulations we use the same initial conditions for the system and state used in the Letter:
initial_field = np.sqrt(0.05) # Note n_0 = <a^dagger a>(0) = 0.05
initial_state = np.array([[0,0],[0,1]]) # spin down
To reduce the computation time we simulate only the first 0.3 ps of the dynamics with much rougher convergence parameters compared to the letter.
tempo_parameters = oqupy.TempoParameters(dt=3.2e-3, dkmax=20, epsrel=10**(-5))
start_time = 0.0
end_time = 0.3
The oqupy.TempoWithField.compute method may then be used to compute
the dynamics in exactly the same way a call to oqupy.Tempo.compute
is used to compute the dynamics for an ordinary System or
TimeDependentSystem:
tempo_sys = oqupy.TempoWithField(system=system,
bath=bath,
initial_state=initial_state,
initial_field=initial_field,
start_time=start_time,
parameters=tempo_parameters)
dynamics_with_field = tempo_sys.compute(end_time=end_time)
--> TEMPO-with-field computation:
100.0% 93 of 93 [########################################] 00:00:17
Elapsed time: 17.9s
TempoWithField.compute returns a DynamicsWithField object
containing both the state matrices and field values at each timestep, in
addition to the timesteps themselves:
times = dynamics_with_field.times
states = dynamics_with_field.states
fields = dynamics_with_field.fields
We plot a the square value of the fields i.e. the photon number, producing the first part of a single line of Fig. 2a.:
n = np.abs(fields)**2
plt.plot(times, n, label=r'$\Gamma_\uparrow = 0.8\Gamma_\downarrow$')
plt.xlabel(r'$t$ (ps)')
plt.ylabel(r'$n/N$')
plt.ylim((0.0,0.15))
plt.legend(loc='upper left')
<matplotlib.legend.Legend at 0x7f4ca4982ba8>
If you have the time you can calculate the dynamics to
\(t=1.3\,\text{ps}\) as in the Letter and check that, even for these
very rough parameters, the results are reasonable close to being
converged with respect to dt, dkmax and epsrel.
While you could repeat the TEMPO computation for each pump strength \(\Gamma_\uparrow\) appearing in Fig. 2a., a more efficient solution for calculating dynamics for multiple sets of system parameters (in this case Lindblad rates) is provided by PT-TEMPO.
4. PT-TEMPO computation for multiple sets of dynamics
The above calculation can be performed quickly for many-different pump strengths \(\Gamma_\uparrow\) using a single process tensor.
As discussed in the Supplement Material for the Letter, there is no guarantee that computational parameters that gave a set of converged results for the TEMPO method will give converged results for a PT-TEMPO calculation. For the sake of this tutorial however let’s assume the above parameters continue to be reasonable. The process tensor to time \(t=0.3\,\text{ps}\) is calculated using these parameters and the bath via
process_tensor = oqupy.pt_tempo_compute(bath=bath,
start_time=0.0,
end_time=0.3,
parameters=tempo_parameters)
--> PT-TEMPO computation:
100.0% 93 of 93 [########################################] 00:00:06
Elapsed time: 6.1s
Refer the Time Dependence and PT-TEMPO tutorial for further discussion of the process tensor.
To calculate the dynamics for the 4 different pump strengths in Fig.
2a., we define a separate system with field object for each pump
strength. Only the gammas array needs to be modified constructor
calls:
pump_ratios = [0.2, 0.4, 0.6, 0.8]
systems = []
for ratio in pump_ratios:
Gamma_up = ratio * Gamma_down
# N.B. a default argument is used to avoid the late-binding closure issue
# discussed here: https://docs.python-guide.org/writing/gotchas/#late-binding-closures
gammas = [ lambda t: Gamma_down, lambda t, Gamma_up=Gamma_up: Gamma_up]
# Use the same Hamiltonian, equation of motion and Lindblad operators
system = oqupy.TimeDependentSystemWithField(H_MF,
field_eom,
gammas=gammas,
lindblad_operators=lindblad_operators)
systems.append(system)
We can then use compute_dynamics_with_field to compute the dynamics
at each \(\Gamma_\uparrow\) for the particular initial condition
using the process tensor calculated above:
t_list = []
n_list = []
for i,system in enumerate(systems):
dynamics = oqupy.compute_dynamics_with_field(
process_tensor=process_tensor,
system=system,
initial_state=initial_state,
initial_field=initial_field,
start_time=0.0)
t = dynamics.times
fields = dynamics.fields
n = np.abs(fields)**2
t_list.append(t)
n_list.append(n)
--> Compute dynamics with field:
100.0% 93 of 93 [########################################] 00:00:13
Elapsed time: 13.8s
--> Compute dynamics with field:
100.0% 93 of 93 [########################################] 00:00:13
Elapsed time: 13.7s
--> Compute dynamics with field:
100.0% 93 of 93 [########################################] 00:00:14
Elapsed time: 14.4s
--> Compute dynamics with field:
100.0% 93 of 93 [########################################] 00:00:13
Elapsed time: 13.8s
Finally, plotting the results:
for i,n in enumerate(n_list):
ratio = pump_ratios[i]
label = r'$\Gamma_\uparrow = {}\Gamma_\downarrow$'.format(pump_ratios[i])
plt.plot(t_list[i], n_list[i], label=label)
plt.xlabel(r'$t$ (ps)')
plt.ylabel(r'$n/N$')
plt.ylim((0.0,0.15))
plt.legend(loc='upper left')
<matplotlib.legend.Legend at 0x7f4ca48cab38>